Simulating Open Loop Gain

Open loop gain is a crucial parameter of an op-amp amplifier. While designing the feedback network around it assuming infinite loop gain is easy to do, one, sometimes, needs to know the poles and open loop gain of the amplifier in order to do frequency compensation, or know what the out-of-band loop gain is, as it might also be important for specifications.

This article will show the solution about how to measure the open loop gain of an op-amp in an accurate and, more importantly, simple manner.

The Open Loop Gain Testbench

TL;DR: This is the solution.

A correct and simple testbench for simulating the Open-Loop Gain of an Op-Amp (in this case, the OP07) is shown in figure 1

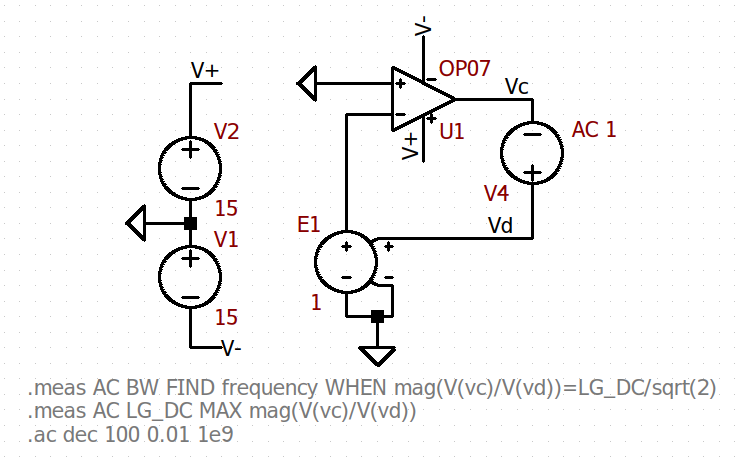
Some people might recognize this method of placing the voltage source along the feedback loop from this Linear Technology of Kris Lokere. Even though it is not metioned there, this is the Middlebrook method (published by him in ’75) with a single voltage source.

We have used an ideal voltage-controlled voltage source (VCVS) and an AC stimuli within the loop.

Why do we need a VCVS with a voltage gain of 1? Isn’t it enough without it? Since we are looking for the open loop gain, then this presumes that the amplifier is not loaded with its own feedback network or some other load. The aim is to keep a DC feedback path while not loading the output of the amplifier.

If we discarded the VCVS, then we would be measuring the loop gain of an standard Op-Amp voltage buffer. If the Op-Amp were really an ideal VCVS with a finite gain, then, using the VCVS with a voltage gain of 1 would be unnecessary. However, a real Op-Amp has a finite input capacitance and resistance. While it is true that these might only make a difference at high frequencies, it is always good to not make any assumptions and test open loop gain properly.

Another well-known Open-Loop Gain Testbench Alternative

Another possibility, as also shown in this TI training video, is as follows:

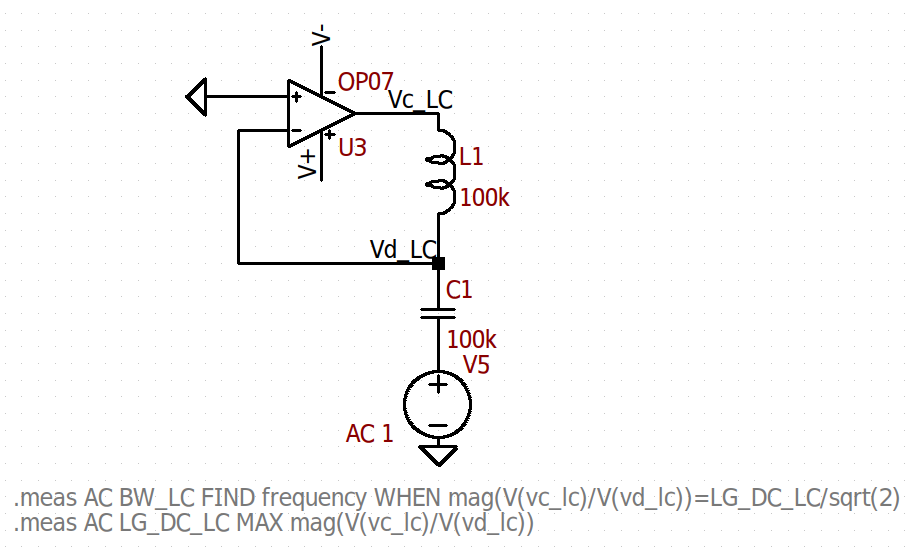
In this case, the voltage souce is placed outside the loop, but an inductor is placed to keep the loop biased at DC (in this case, the output and (-) port and output are at 0V). However, it also isolates the input (-) port and the output at AC, as it represents a very high impedacne. A capacitor is used in series with the voltage source in order to not disturb the Op-Amp biasing with the DC bias of the source.

Comparison

To prove that both TBs give out the same simulation results, we run them in LTspice and compare its frequency response and calculated low-frequency open loop gain and dominant pole.

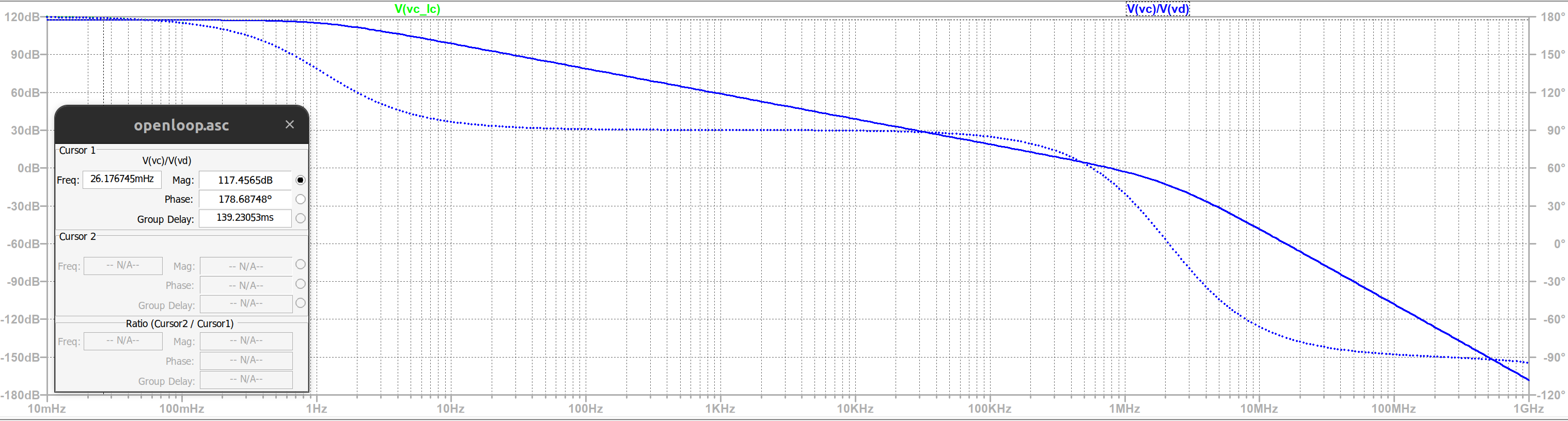
In figure 4, the dominant pole is calculated under the “bw” and “bw_lc” (for the method with L and C) variables, and the maximum open loop gain is under “lg_dc” or “lg_dc_lc”.

Both calculations result in 1.1Hz as a the location of the dominant pole and 117.46dB as the open loop gain at low frequencies (below the pole).

To conclude, both results are equally valid and correct. Perhaps the method with the VCVS might be sligtly simpler as it uses only 2 extra elements (besides the op-amp itself) to evaluate open loop gain, whereas the L and C method needs 3 (the L, C and voltage source). It’s not an important difference, anyhow, so both methods can be used interchangeably.

Modeling Conclusion

Since we have calculated the dominant pole location and the open loop gain at low frequencies, we can model the op-amp open loop gain formula as: \[\begin{aligned}
A_{OL}(s) = \frac{746.448k}{1+\frac{s}{2\pi1.1Hz}}
\end{aligned}\]

To verify this claim, we model the op-amp open loop gain with a VCVS source in ltspice, as shown in figure 5.

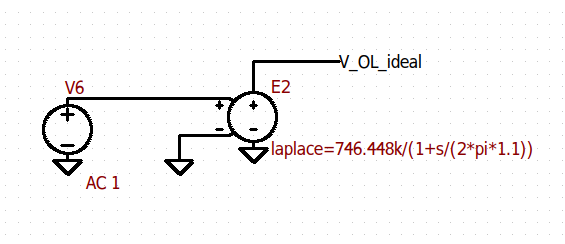
We run an AC simulation and overlay this open loop gain with the previous measured result, results are shown in figure 6.

The blue curve in figure 6 is the ideal model. Obviously, we have only come up with a 1st-order model, as there’s a second pole below the 0dB line that has not been model. Therefore, we can claim that our model is good enough to 1st-order.